R2U2 Implementation

R2U2 Implementation#

Abstract Syntax Tree Architecture#

R2U2 is a stream-based runtime monitor that reevaluates MLTL and ptMLTL formulas for each time index \(i\). The Configuration Compiler for Property Organization (C2PO) [1] compiles MLTL and ptMLTL formula(s) for input into R2U2. C2PO decomposes the MLTL and ptMLTL formula(s) into subformula nodes represented in an Abstract Syntax Tree (AST) and optimizes the AST by applying Common Subexpression Elimination [1] [2] and various rewriting rules [3]. C2PO then outputs assembly-style instructions for R2U2 to reason over. The figures below illustrate an AST and the compiled instructions for \((\Box_{[0,3]}\psi)\ \mathcal{U}_{[2,4]}\ \xi\).

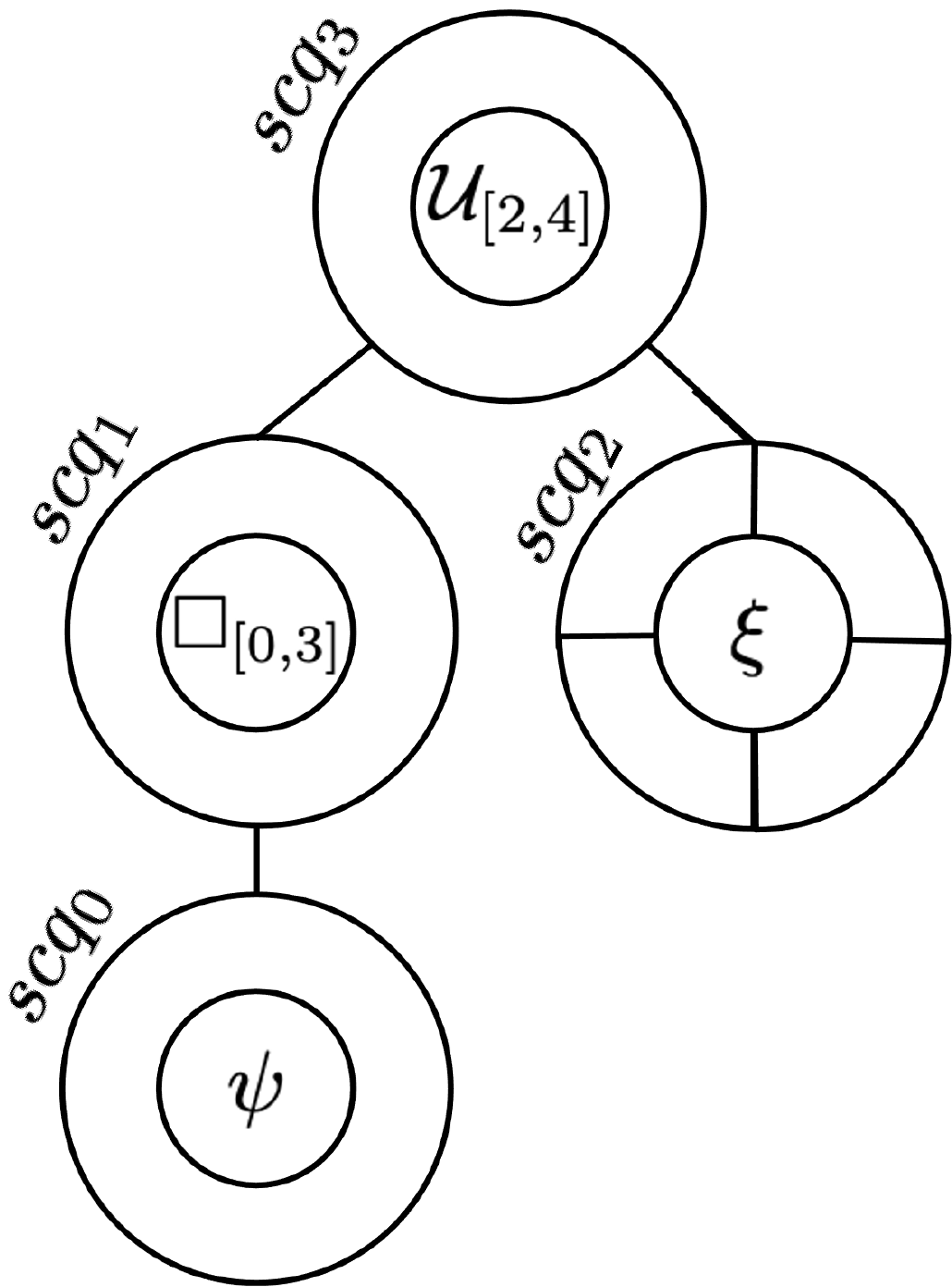
../_images/SCQ.png

AST for \((\Box_{[0,3]}\psi)\ \mathcal{U}_{[2,4]}\ \xi\)#

../_images/AssemblyInstructions.png

Instructions compiled by C2PO for \((\Box_{[0,3]}\psi)\ \mathcal{U}_{[2,4]}\ \xi\). Instructions 0–3 are the computation instructions (blue), and instructions 4–9 are the configuration instructions (red)#

In the outputted assembly, there are configuration instructions and computation instructions. The configuration instructions are run once upon initialization to configure the AST in terms of sizing and metadata (e.g., the lower and upper bounds of temporal operators). The computation instructions are saved in a table and sequentially iterated over at each timestamp. The computation instructions are ordered such that R2U2 reasons over the AST by determining the evaluation of each subformula node from the bottom-up and propagating verdicts to the parent node(s).

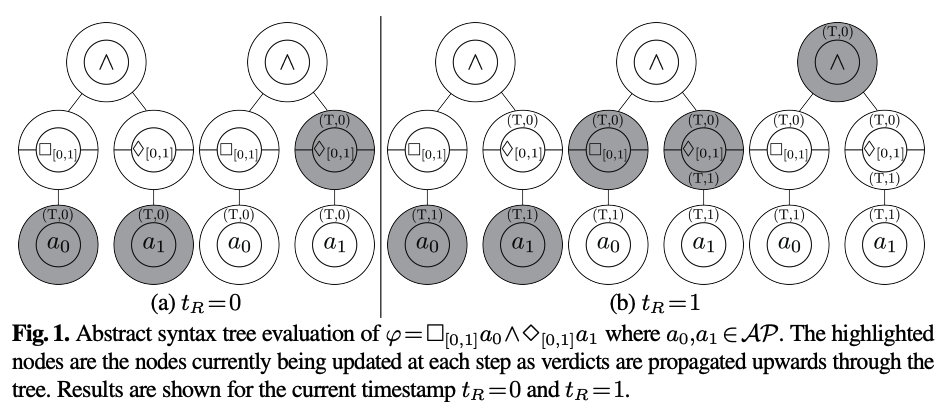
Each node of the AST computes and stores verdict-timestamp tuples \(T_{\varphi} = (v, \tau)\) for its subformula \(\varphi\), where \(v \in \{\sf true, \sf false\}\) and \(\tau \in \mathcal{N}_0\). Each node stores the verdict-timestamp tuples in a shared connection queue (SCQ), where the SCQ is a circular buffer that overwrites verdict-timestamp tuples in a circular and aggregated manner. Fig. 1 below demonstrates an example of how R2U2 evaluates over an AST.

../_images/ASTEvaluation.png

Shared Connection Queue (SCQ)#

We employ what we call SCQs to store subformula results. An SCQ is a circular buffer with one write pointer and one or more read pointers.There are two reasons we use the SCQ: 1) Each subformula may produce more than one tuple; 2) more than one parent nodes may read data from a given subformula.

A verdict-timestamp tuple \(T_\varphi = (v, \tau)\) is stored in \(\varphi\)’s SCQ using aggregation [2] [4]. Aggregation occurs such that if an incoming tuple’s verdict \(v\) is equivalent to the previous tuple’s verdict \(v\), then the incoming tuple’s timestamp \(\tau\) overwrites the previous tuple’s timestamp \(\tau\). For example, if \(\varphi\)’s SCQ contains \(\{(\sf true,3), (\sf false,7)\}\), then \(\varphi=\sf false\) for the entire timestamp interval \([4,7]\), and if \(\varphi\) encounters an incoming tuple \(T_\varphi = (\sf false, 8)\), then \(\varphi\)’s SCQ becomes \(\{(\sf true,3), (\sf false,8)\}\). This aggregated storing of verdict-timestamp tuples allows R2U2 to easily reason over multiple timestamps (with equivalent verdicts) at once. The SCQ write and read algorithms (along with proofs of correctness) are given in [5].

SCQ Utilization#

To compute the SCQ size of each node in the AST, the propagation delay of each subformula must first be computed.

Propagation Delay [2]: The propagation delay of an MLTL or ptMLTL formula \(\varphi\) is the time between when a set of propositions \(\pi(i)\) arrives and when the verdict of \(\pi, i \models \varphi\) is determinable. The best-case propagation delay (\(\varphi.bpd\)) is its minimum time delay, and the worst-case propagation delay (\(\varphi.wpd\)) is its maximum time delay. \end{definition}

MLTL Propagation Delay Semantics [2]: Let \(\psi\) and \(\xi\) be subformulas of an MLTL formula \(\varphi\) where \(\varphi.bpd\) and \(\varphi.wpd\) are structurally defined as follows:

\[\begin{equation*} \begin{split} &\text{ $\bullet$ $\varphi\in \mathcal{AP}$}: \begin{cases} \varphi.wpd = 0\\ \varphi.bpd = 0\\ \end{cases}\\ &\text{$\bullet$ $\varphi=\neg \psi$}: \begin{cases} \varphi.wpd = \psi.wpd\\ \varphi.bpd = \psi.bpd\\ \end{cases}\\ &\text{ $\bullet$ $\varphi=\psi\ \vee\ \xi$ $ or $ $\varphi=\psi\ \wedge\ \xi$}: \begin{cases} \varphi.wpd = max(\psi.wpd,\ \xi.wpd)\\ \varphi.bpd = min(\psi.bpd,\ \xi.bpd)\\ \end{cases}\\ &\text{ $\bullet$ $\varphi=\Box_{[lb,ub]} \psi$ $ or $ $\varphi=\Diamond_{[lb,ub]} \psi$}: \begin{cases} \varphi.wpd = \psi.wpd+ub\\ \varphi.bpd = \psi.bpd+lb\\ \end{cases}\\ &\text{ $\bullet$ $\varphi=\psi\ \mathcal{U}_{[lb,ub]\ }\xi$ $ or $ $\varphi=\psi\ \mathcal{R}_{[lb,ub]}\ \xi$}: \begin{cases} \varphi.wpd = max(\psi.wpd,\ \xi.wpd)+ub\\ \varphi.bpd = min(\psi.bpd,\ \xi.bpd)+lb\\ \end{cases}\\ \end{split} \end{equation*}\]

ptMLTL Propagation Delay Semantics [5]: Let \(\psi\) and \(\xi\) be subformulas of a ptMLTL formula \(\varphi\) where \(\varphi.bpd\) and \(\varphi.wpd\) are structurally defined as follows:

\[\begin{equation*} \begin{split} &\text{ $\bullet$ $\varphi\in \mathcal{AP}$}: \begin{cases} \varphi.wpd = 0\\ \varphi.bpd = 0\\ \end{cases}\\ &\text{$\bullet$ $\varphi=\neg \psi$}: \begin{cases} \varphi.wpd = \psi.wpd\\ \varphi.bpd = \psi.bpd\\ \end{cases}\\ &\text{ $\bullet$ $\varphi=\psi\ \vee\ \xi$ $ or $ $\varphi=\psi\ \wedge\ \xi$}: \begin{cases} \varphi.wpd = max(\psi.wpd,\ \xi.wpd)\\ \varphi.bpd = min(\psi.bpd,\ \xi.bpd)\\ \end{cases}\\ &\text{ $\bullet$ $\varphi=\mathcal{H}_{[lb,ub]} \psi$ $ or $ $\varphi=\mathcal{O}_{[lb,ub]} \psi$}: \begin{cases} \varphi.wpd = \psi.wpd-lb\\ \varphi.bpd = \psi.bpd-ub\\ \end{cases}\\ &\text{ $\bullet$ $\varphi=\psi\ \mathcal{S}_{[lb,ub]\ }\xi$ $ or $ $\varphi=\psi\ \mathcal{T}_{[lb,ub]}\ \xi$}: \begin{cases} \varphi.wpd = max(\psi.wpd,\ \xi.wpd)-lb\\ \varphi.bpd = min(\psi.bpd,\ \xi.bpd)-lb\\ \end{cases}\\ \end{split} \end{equation*}\]

To minimize the required memory resources of R2U2, the SCQs are minimally sized such that the SCQ will never overwrite a verdict-timestamp tuple required by its parent node. The minimum SCQ size of an AST node \(\varphi\) is determined by the worst-case propagation delay of its sibling nodes and its own best-case propagation delay; in the worst case, a node \(\varphi\) must store verdict-timestamp tuples in its SCQ until all of \(\varphi\)’s siblings have the same timestamp \(\tau\) for these tuples to be consumed by their parent node. Therefore, the size of node \(\varphi\)’s SCQ corresponds to the maximum timestamp mismatch between node \(\varphi\) and \(\varphi\)’s siblings. Let \(\mathbb{S}_\varphi\) be the set of all of \(\varphi\)’s sibling nodes, then the size of \(\varphi\)’s SCQ is given by the following (proof available in [6]):

(1)#\[\begin{equation} SCQ_{size}(\varphi) = max(max\{s.wpd\text{ $|$ } s \in \mathbb{S}_\varphi\}-\varphi.bpd,\ 0)+1 \end{equation}\]

Operators#

For more details on operator definitions, see [5] and [2].

References#

Contents